이번에는 코딩테스트의 기초로 유명한 DFS 를 볼 것이다
DFS 알고리즘 이란?
DFS (Depth First Search)는 깊이 우선탐색으로 그래프나 트리에서 사용되는 알고리즘이다.
주로 한 노드에서 출발해서 연결된 모든 노드를 방문하는 방법으로 BFS와 같이 사용하게 된다.
간단하게 말하자면 한 노드에서 시작할때 가능한 한 깊게 노드를 탐색하고, 더 이상 탐색할 곳이 없을때 다음 분기점으로 넘어가 경로를 탐색하는 것이다.
DFS 알고리즘 작동 방식
DFS 알고리즘이 어떻게 진행되는지를 한번 살펴보자
- 시작 노드 방문
- 인접 노드 탐색 (가능한 깊이까지)
- 되돌아가기
- 반복하기
위의 순서대로 진행하게 된다.
이 알고리즘은 특수한 배열이 하나 필요한데 이 노드가 방문되었는지를 확인하는 visited 배열이다.
만일 2번의 인접 노드를 탐색하는데 그 노드가 이미 방문되었다면? 그 노드를 건너뛰고 다른 노드들을 탐색하게 되는 것이다.
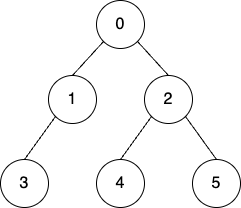
위와 같은 그래프이자 트리가 있다고 가정해보자. 위 간선들은 양방향이다.
이때 시작노드는 0으로 정하도록 한다.
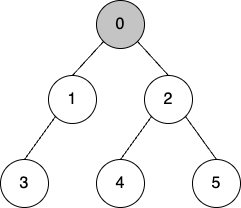
- 시작 노드 방문
- visited = [0]
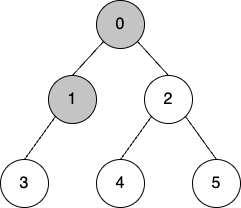
2. 인접 노드 탐색
- 인접 노드가 1, 2 두개가 있지만 DFS는 먼저 온 1부터 탐색하게 된다.
- visited = [0, 1]
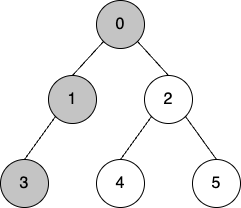
2-1. 인접 노드 탐색 (가능한 깊이까지)
- 가능한 깊이까지 가야하므로 1의 인접노드인 3을 탐색한다
- visited = [0, 1, 3]
3. 되돌아가기
- 더 이상 탐색할 수 없으므로 마지막 분기점인 0에서 이번엔 2를 탐색하게 된다.
4. 반복하기
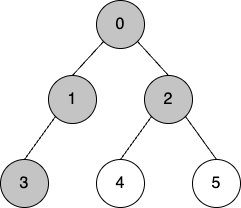
2. 인접 노드 탐색
- 0의 다음 인접노드인 2를 탐색한다
- visited = [0, 1, 3, 2]
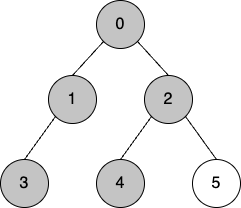
2-1. 인접 노드 탐색
- 2의 인접노드 4를 탐색한다.
- visited = [0, 1, 3, 2, 4]
3. 되돌아가기
- 4를 탐색할 수 없으므로 2로 되돌아간다.
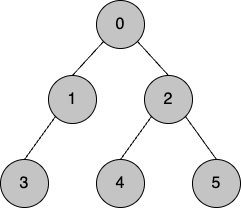
2. 인접노드 탐색
- 마지막 노드인 5를 탐색하고 마무리한다.
결론
깊이 우선 탐색은 가능한 모든 깊이를 탐색하기 때문에
0 -> 1 -> 3 -> 2 -> 4 -> 5 순서대로 탐색한다.
어떤 문제에서 DFS를 써야하는가
DFS문제들은 주로 딱보면 깊이 우선 탐색을 해야할 것 같은데? 라는 느낌이 들긴하지만 어떤 문제에서 사용하는 것이 좋은지 살펴보았다.
- 경로 탐색( ex 미로찾기)
- 그래프 내의 사이클 찾기
- 그래프 내의 여러 개의 분리된 부분 찾기 (사이클과 유사)
- 위상정렬 (topological sort)
즉 주로 그래프 문제에서 사용한다 정도로 정리할 수 있겠다.
단 위의 경로 탐색에서 최단경로 문제는 BFS를 사용하는 것이 맞고, DFS는 이 경로가 가능한가? (사이클 인가) 를 판단하는데 사용하는게 맞는 것 같다.
DFS 알고리즘 장단점 / 시간복잡도
장점
- BFS보다 메모리 효율적이다.
- 구현이 간단하다.
단점
- 최단 경로를 구할 수는 없다
사실 BFS의 단점은 DFS의 장점, DFS의 장점은 BFS의 단점이라고 할 수 있다.
넓이 우선탐색은 가능한 모든 노드를 넣어두고 시작하기 때문에 상대적으로 메모리를 많이 쓴다고 볼 수 있고, 역시 BFS는 특성상 처음 도달하는 방법이 최단 경로이다.
시간복잡도
노드수(V), 간선수 (E) 일때
O(V+E) 의 시간복잡도를 가지게 된다.
C++ DFS 알고리즘 구현
DFS 알고리즘을 구현하는 방법은 재귀, 스택 두가지 방법이 있는데
개인적으로는 스택이 좀 더 편하고 직관적인 것 같다.
재귀는 잘못 사용하면 터질 것 같아서 불안하다. ㅎ
DFS 알고리즘 재귀
void DFS(int u, vector<int> adj[], vector<bool>& visited) {
visited[u] = true;
cout << u << " ";
// 인접한 모든 노드를 반복
for (int i = 0; i < adj[u].size(); i++) {
if (!visited[adj[u][i]]) {
DFS(adj[u][i], adj, visited); // 방문하지 않은 노드에 대해 DFS 수행
}
}
}
재귀함수는 위와 같은데, u는 시작 노드, adj는 간선들의 배열이다.
adj[u]라고 한다면 u 노드와 연결되어 있는 간선들을 모아놓은 것이다.
visited는 앞서 설명한 방문한 노드이다.
- 시작 노드 방문
- 인접 노드가 방문하지 않은 노드인 경우 인접 노드 탐색
- 재귀 호출
시작 노드를 방문한 뒤, 시작 노드와 연결된 다음 인접노드가 방문되지 않았을 경우 해당 노드를 시작 노드로 해서 다시 재귀로 함수를 실행한다.
DFS 알고리즘 stack
void DFS(int V, vector<int> adj[], int start) {
vector<bool> visited(V, false);
stack<int> stack;
stack.push(start);
while (!stack.empty()) {
int u = stack.top();
stack.pop();
if (!visited[u]) {
visited[u] = true;
cout << u << " ";
for (int i = 0; i < adj[u].size(); i++) {
if (!visited[adj[u][i]]) {
stack.push(adj[u][i]);
}
}
}
}
}
보통 DFS는 stack을 사용해서 구현하는 경우가 많긴 하지만
앞서 본 재귀가 좀더 코드가 간결하긴 하다.
이번에는 시작노드를 stack 에 push 하고 시작한다.
그 후 stack에서 노드를 pop해서 그 노드가 방문하지 않았었다면 방문처리하고, 인접노드들을 모두 stack에 push해준다.
위의 과정을 노드가 존재한다면 (방문하지 않은 노드가 있다면) 계속 반복한다.
재귀는 인접노드 하나씩 실행한 결과라면, stack에서는 하나의 노드의 인접노드들을 stack에 한꺼번에 넣고 하나씩 꺼내쓴다는 점이 보인다.




